Appendix E — Skill Assignment 5: EDA 2+ variables & hypothesis testing

Author

Methods Student

Published

November 13, 2024

Find Quarto themes here.

Find the sample assignment here.

E.1 Overall Discussion

I ran three graphs using my recoded Roe v. Wade variable.

  • Hypothesis 1: The more conservative a person is the more likely they will be to support overturning Roe v. Wade.

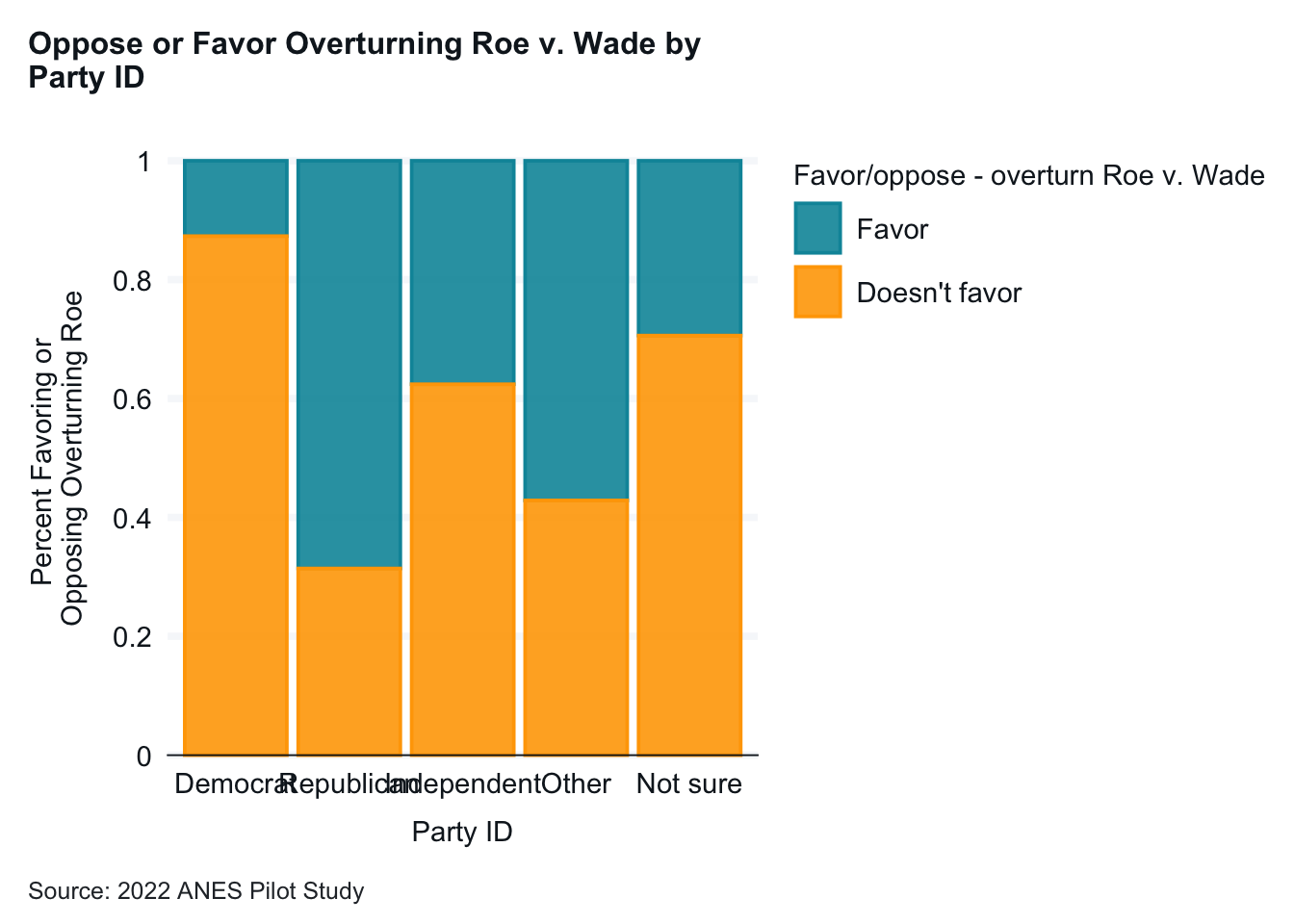
  • The first graph looked at whether support (or opposition) to overturning Roe varied by political party. Almost all Democrats opposed overturning Roe. A smaller majority of Republicans favored overturning Roe. The other groups were in the middle.

  • Hypothesis test: The relationship between party ID and reaction to Roe v. Wade being overturned is statistically significant. p = .000 so we can reject the null hypothesis. Cramer’s V is .469. This is high and tells us that the relationship is also strong. The numbers in the table bear this out as well. For example, only 15.8% of Democrats favor overturning Roe, while 69.8% of Republicans do. Independent voters are in between, with 36.5% favoring Roe. The hypothesis is confirmed. We can reject the null hypothesis.

    Don’t forget to write up each of the hypothesis tests, not just the first one! Here are interpretations of each graph.

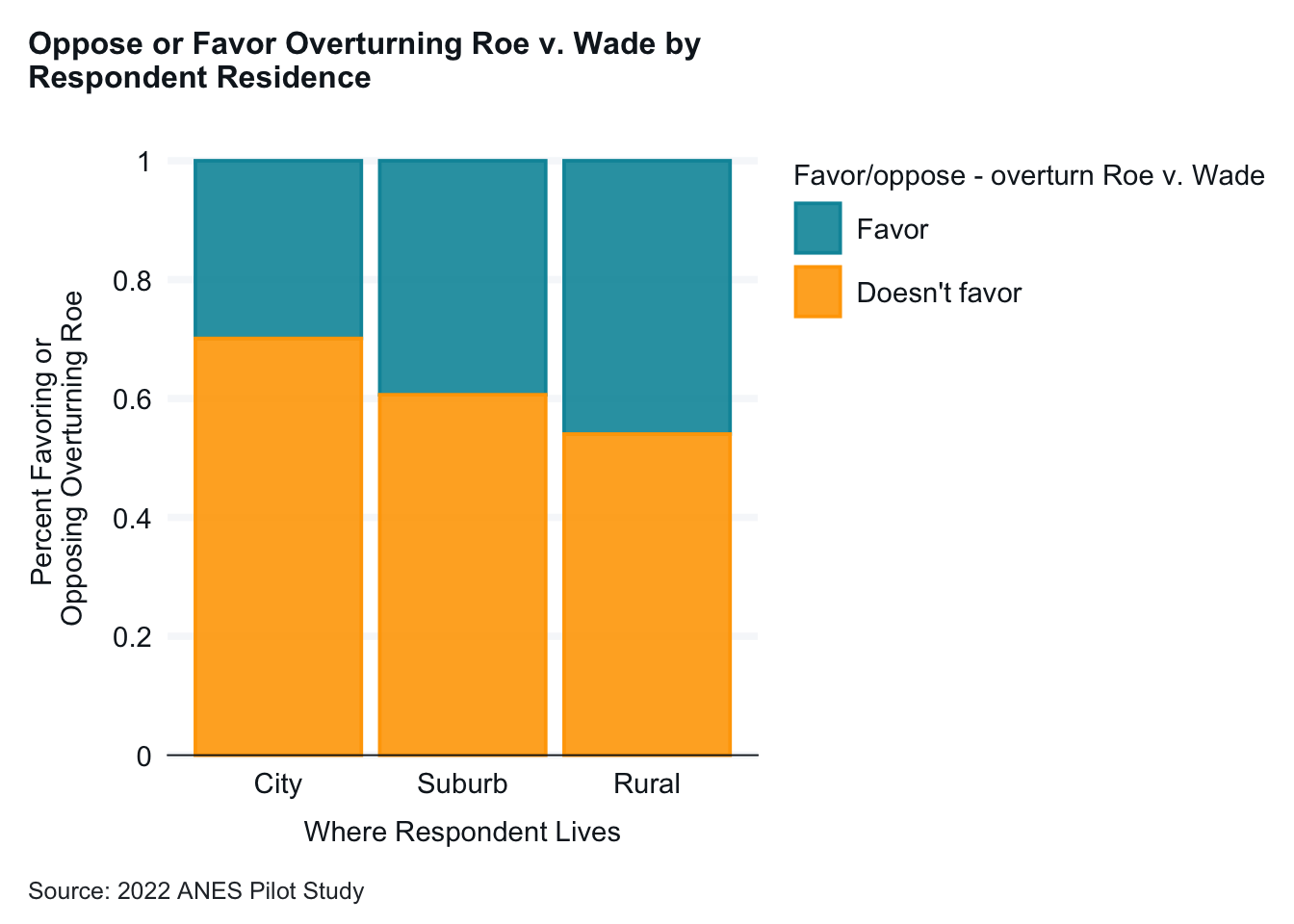
  • The second graph looked at whether support (or opposition) to overturning Roe varied by where people lived. All groups had majorities of people who didn’t favor overturning Roe. People lived in cities had the largest majorities, followed by suburban and rural Americans. The differences between the three groups were not as large as with party differences.

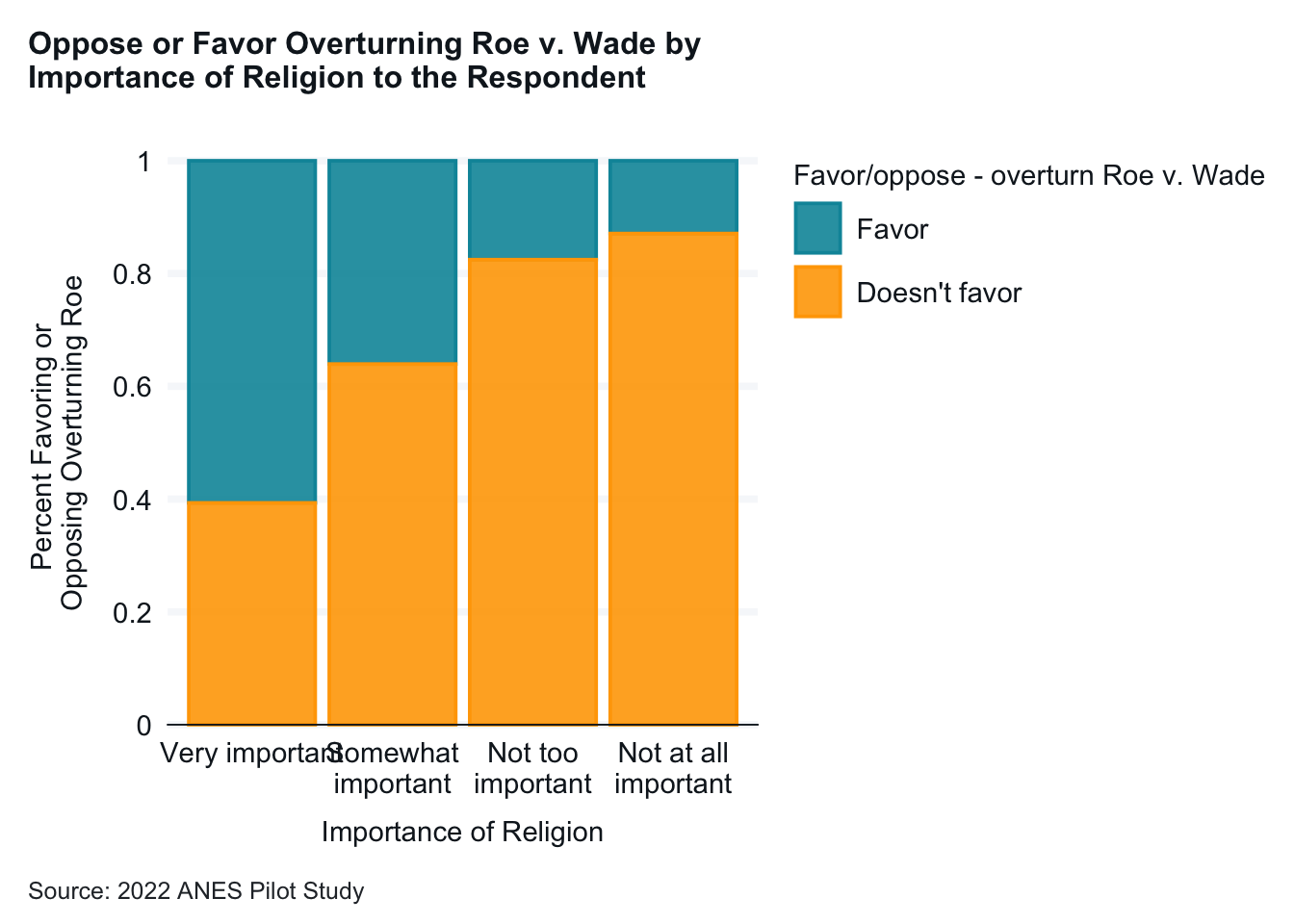
  • The third graph examined whether support (or opposition) to overturning Roe varied by the importance of religion in people’s lives. Majority of people for whom religion is very important favored overturning Roe. For the other groups a majority didn’t favor overturning Roe. The percent of opposition went up as religion was less important in people’s lives.

  • None of the results I found surprised me.

E.1.1 Load Packages

library(tidyverse)
library(haven)
library(hrbrthemes)
library(survey)
library(srvyr)
library(labelled)
library(sjmisc)
library(sjPlot)
library(gmodels)
library(gtsummary)
library(skimr)
library(ggblanket)

set_blanket()

E.1.2 Load Your Dataset

Need help? Go to chapter x in the webbook.

load("another_anes_pilot_smaller_2.RData")

E.1.3 Manage your data as needed

Need help? Go to chapter x in the webbook.

E.1.4 Graph & Cross-tab 1

Need help? Go to chapter 4 in the webbook.

another_anes_pilot_smaller_2 |>
  #filter(pid3 == "Democrat" | pid3 == "Republican") |>
  #mutate(pid3 = forcats::fct_drop(pid3)) |> 
  as_factor() |>
  drop_na(pid3, roe_recode) |>
  gg_bar(
    x = pid3,
    col = roe_recode,
    position = "fill",
    title = "Oppose or Favor Overturning Roe v. Wade by \nParty ID",
    caption = "Source: 2022 ANES Pilot Study",
    col_title = "Overturn Roe v. Wade", 
    x_labels =  \(x) str_wrap(x, width = 15)
  ) +
  labs(x = "Party ID", 
       y = "Percent Favoring or \nOpposing Overturning Roe"
)

another_anes_pilot_smaller_2 |>
  select(roe_recode, pid3) |>
  sjtab(fun = "xtab", 
        show.col.prc = TRUE)
Favor/oppose -
overturn Roe v. Wade		 Profile: 3 point
Party ID		 Total
Democrat Republican Independent Other Not sure
Favor 54
12.7 %		 238
68.6 %		 100
37.6 %		 24
57.1 %		 5
29.4 %		 421
38.3 %
Doesn't favor 372
87.3 %		 109
31.4 %		 166
62.4 %		 18
42.9 %		 12
70.6 %		 677
61.7 %
Total 426
100 %		 347
100 %		 266
100 %		 42
100 %		 17
100 %		 1098
100 %
χ2=259.893 · df=4 · Cramer's V=0.487 · p=0.000

E.1.5 Graph & Cross-tab 2

 another_anes_pilot_smaller_2 |>
   as_factor() |>
   drop_na(urbanicity2_recode, roe_recode) |>
   gg_bar(
    x = urbanicity2_recode,
    col = roe_recode,
    position = "fill",
    title = "Oppose or Favor Overturning Roe v. Wade by \nRespondent Residence",
    caption = "Source: 2022 ANES Pilot Study",
    col_title = "Overturn Roe v. Wade", 
    x_labels =  \(x) str_wrap(x, width = 15)
  ) +
   labs(x = "Where Respondent Lives", 
        y = "Percent Favoring or \nOpposing Overturning Roe"
)

another_anes_pilot_smaller_2 |>
  select(roe_recode, urbanicity2_recode) |>
  sjtab(fun = "xtab", 
        show.col.prc = TRUE)
Favor/oppose -
overturn Roe v. Wade		 Profile: Urban-rural
status		 Total
City Suburb Rural
Favor 113
29.9 %		 161
39.4 %		 160
46 %		 434
38.2 %
Doesn't favor 265
70.1 %		 248
60.6 %		 188
54 %		 701
61.8 %
Total 378
100 %		 409
100 %		 348
100 %		 1135
100 %
χ2=20.188 · df=2 · Cramer's V=0.133 · p=0.000

E.1.6 Graph & Cross-tab 3 (add more if you want to!)

 another_anes_pilot_smaller_2 |>
   as_factor() |>
   drop_na(pew_religimp, roe_recode) |>
   gg_bar(
    x = pew_religimp,
    col = roe_recode,
    position = "fill",
    title = "Oppose or Favor Overturning Roe v. Wade by \nImportance of Religion to the Respondent",
    caption = "Source: 2022 ANES Pilot Study",
    #col_title = "Overturn Roe v. Wade", 
    x_labels =  \(x) str_wrap(x, width = 15)
  ) +
   labs(x = "Importance of Religion", 
        y = "Percent Favoring or \nOpposing Overturning Roe"
)

another_anes_pilot_smaller_2 |>
  select(roe_recode, pew_religimp) |>
  sjtab(fun = "xtab", 
        show.col.prc = TRUE)
Favor/oppose -
overturn Roe v. Wade		 Profile: Importance
of religion (Pew
version)		 Total
Very important Somewhat important Not too important Not at all important
Favor 273
60.7 %		 102
36 %		 27
17.5 %		 32
12.9 %		 434
38.2 %
Doesn't favor 177
39.3 %		 181
64 %		 127
82.5 %		 216
87.1 %		 701
61.8 %
Total 450
100 %		 283
100 %		 154
100 %		 248
100 %		 1135
100 %
χ2=191.788 · df=3 · Cramer's V=0.411 · p=0.000

E.2 Discussion

Hypothesis 1: The more conservative a person is the more likely they will be to support overturning Roe v. Wade.

Hypothesis test 1: The relationship between party ID and reaction to Roe v. Wade being overturned is statistically significant. p = .000 so we can reject the null hypothesis. Cramer’s V is .469. This is high and tells us that the relationship is also strong. The numbers in the table bear this out as well. For example, only 15.8% of Democrats favor overturning Roe, while 69.8% of Republicans do. Independent voters are in between, with 36.5% favoring Roe. The hypothesis is confirmed. We can reject the null hypothesis.

Don’t forget to write up each of the hypothesis tests, not just the first one!

E.3 Load Packages

library(tidyverse)
library(haven)
library(hrbrthemes)
library(survey)
library(srvyr)
library(labelled)
library(sjmisc)
library(sjPlot)
library(gmodels)
library(gtsummary)
library(skimr)
library(ggblanket)
library(emmeans)

E.4 Load Your Dataset

Need help? Go to chapter 5 in the webbook.

load("another_anes_pilot_smaller_2.RData")

E.5 Manage your data as needed

Need help? Go to chapter 6 in the webbook.

E.6 Hypothesis Test 1

Need help? Go to chapter 11 in the webbook.

another_anes_pilot_smaller_2 |>
  select(roe_recode, pid3) |>
  sjtab(fun = "xtab", 
        show.col.prc = TRUE)
Favor/oppose -
overturn Roe v. Wade		 Profile: 3 point
Party ID		 Total
Democrat Republican Independent Other Not sure
Favor 54
12.7 %		 238
68.6 %		 100
37.6 %		 24
57.1 %		 5
29.4 %		 421
38.3 %
Doesn't favor 372
87.3 %		 109
31.4 %		 166
62.4 %		 18
42.9 %		 12
70.6 %		 677
61.7 %
Total 426
100 %		 347
100 %		 266
100 %		 42
100 %		 17
100 %		 1098
100 %
χ2=259.893 · df=4 · Cramer's V=0.487 · p=0.000 
model_1 <- glm(roe_recode ~ pid3, family = "binomial", data = another_anes_pilot_smaller_2, weights = weight)
emmeans(model_1, pairwise ~ pid3)$contrasts
 contrast                 estimate    SE  df z.ratio p.value
 Democrat - Republican      2.5142 0.190 Inf  13.244  <.0001
 Democrat - Independent     1.1176 0.197 Inf   5.660  <.0001
 Democrat - Other           2.1309 0.371 Inf   5.745  <.0001
 Democrat - Not sure        1.2091 0.538 Inf   2.247  0.1625
 Republican - Independent  -1.3966 0.185 Inf  -7.555  <.0001
 Republican - Other        -0.3833 0.364 Inf  -1.052  0.8310
 Republican - Not sure     -1.3050 0.534 Inf  -2.446  0.1034
 Independent - Other        1.0133 0.368 Inf   2.750  0.0470
 Independent - Not sure     0.0916 0.536 Inf   0.171  0.9998
 Other - Not sure          -0.9217 0.622 Inf  -1.483  0.5735

Results are given on the log odds ratio (not the response) scale. 
P value adjustment: tukey method for comparing a family of 5 estimates

E.7 Hypothesis Test 2

another_anes_pilot_smaller_2 |>
  select(roe_recode, urbanicity2_recode) |>
  sjtab(fun = "xtab", 
        show.col.prc = TRUE)
Favor/oppose -
overturn Roe v. Wade		 Profile: Urban-rural
status		 Total
City Suburb Rural
Favor 113
29.9 %		 161
39.4 %		 160
46 %		 434
38.2 %
Doesn't favor 265
70.1 %		 248
60.6 %		 188
54 %		 701
61.8 %
Total 378
100 %		 409
100 %		 348
100 %		 1135
100 %
χ2=20.188 · df=2 · Cramer's V=0.133 · p=0.000 
model_2 <- glm(roe_recode ~ urbanicity2_recode, family = "binomial", data = another_anes_pilot_smaller_2, weights = weight)
emmeans(model_2, pairwise ~ urbanicity2_recode)$contrasts
 contrast       estimate    SE  df z.ratio p.value
 City - Suburb     0.406 0.160 Inf   2.544  0.0295
 City - Rural      0.681 0.165 Inf   4.137  0.0001
 Suburb - Rural    0.275 0.158 Inf   1.744  0.1890

Results are given on the log odds ratio (not the response) scale. 
P value adjustment: tukey method for comparing a family of 3 estimates

E.8 Hypothesis Test 3 (add more if needed!)

another_anes_pilot_smaller_2 |>
  select(roe_recode, pew_religimp) |>
  sjtab(fun = "xtab", 
        show.col.prc = TRUE)
Favor/oppose -
overturn Roe v. Wade		 Profile: Importance
of religion (Pew
version)		 Total
Very important Somewhat important Not too important Not at all important
Favor 273
60.7 %		 102
36 %		 27
17.5 %		 32
12.9 %		 434
38.2 %
Doesn't favor 177
39.3 %		 181
64 %		 127
82.5 %		 216
87.1 %		 701
61.8 %
Total 450
100 %		 283
100 %		 154
100 %		 248
100 %		 1135
100 %
χ2=191.788 · df=3 · Cramer's V=0.411 · p=0.000 
model_3 <- glm(roe_recode ~ pew_religimp, family = "binomial", data = another_anes_pilot_smaller_2, weights = weight)
emmeans(model_3, pairwise ~ pew_religimp)$contrasts
 contrast                                  estimate    SE  df z.ratio p.value
 Very important - Somewhat important         -1.039 0.168 Inf  -6.199  <.0001
 Very important - Not too important          -1.899 0.237 Inf  -8.015  <.0001
 Very important - Not at all important       -2.323 0.223 Inf -10.416  <.0001
 Somewhat important - Not too important      -0.860 0.250 Inf  -3.439  0.0033
 Somewhat important - Not at all important   -1.284 0.237 Inf  -5.417  <.0001
 Not too important - Not at all important    -0.424 0.290 Inf  -1.459  0.4623

Results are given on the log odds ratio (not the response) scale. 
P value adjustment: tukey method for comparing a family of 4 estimates

E.8.1 Save your updated dataset?

Need help? Go to chapter 4 in the webbook.